Symposium sur la Sécurité des Techologies de l’Information et des Communications is a security conference held each year in Rennes, France. Each year, they release a challenge usually divided into several smaller tasks. 2017 was my third participation and, just like the previous editions, it has proven to be really challenging and interesting, so I highly recommand giving it a try !
Today’s post will be a write up of the 3rd task. I particuliary enjoyed this one, so I’m gonna share it here.
Background :
Once you complete the first task, you’re given instructions to setup the environment for the rest of the challenge and here’s what it looks like when you’re done doing it :
What’s you’re seeing is an OpenRisk1000 virtual machine written in Javascript (based on the opensource project jor1k) and executed in a web browser. It is worth mentioning the presence of a Trusted Execution Environment (TEE), in the shape of a second virtual machine, this time for the RiscV architecture.
First approach :
The zip archive contains 4 files :
- 2 binaries :
TA.elf.signed: ELF 32-bit LSB executable, UCB RISC-V, version 1 (SYSV), statically linked, not strippedtrustzone_decrypt: ELF 32-bit MSB executable, OpenRISC, version 1 (SYSV), dynamically linked (uses shared libs), not stripped
- 2 encrypted files :
- password_is_00112233445566778899AABBCCDDEEFF.txt.encrypted
- secret.lzma.encrypted
Let’s start by launching the OpenRisk1000 binary to have a quick look at his role :
/challenges/riscy_zones $ ./trustzone_decrypt usage: ./trustzone_decrypt [password] [encrypted file] [destination file]
The program seems responsible for the decryption mechanism, it expects an encrypted file and a password, then it probably writes the decrypted output in the file specified as parameter.
We can try this out with the encrypted file password_is_00112233445566778899AABBCCDDEEFF.txt.encrypted and the password 00112233445566778899AABBCCDDEEFF :
./trustzone_decrypt [password] [encrypted file] [destination file] /challenges/riscy_zones $ ./trustzone_decrypt 00112233445566778899AABBCCDDEEFF password_is_00112233445566778899AABBCCDDEEFF.txt.encrypted test [i] load TA.elf.signed in TrustedOS [+] OS return code = 0x00000000, TA return code = 0x00000000 [i] Send command to Trusted App CMD_GET_TA_VERSION [+] OS return code = 0x00000000, TA return code = 0x00000000 retreived version : SSTIC Trusted APP v0.0.1 [i] check password in TEE [+] OS return code = 0x00000000, TA return code = 0x00000000 Good password ! [i] Send command to Trusted App CMD_DECRYPT_BLOCK [+] OS return code = 0x00000000, TA return code = 0x00000000 [i] Send command to Trusted App CMD_DECRYPT_BLOCK [+] OS return code = 0x00000000, TA return code = 0x00000000 [i] Send command to Trusted App CMD_DECRYPT_BLOCK [+] OS return code = 0x00000000, TA return code = 0x00000000 [i] Send command to Trusted App CMD_DECRYPT_BLOCK [+] OS return code = 0x00000000, TA return code = 0x00000000 [i] Send command to Trusted App CMD_DECRYPT_BLOCK [+] OS return code = 0x00000000, TA return code = 0x00000000 [i] Send command to Trusted App CMD_DECRYPT_BLOCK [+] OS return code = 0x00000000, TA return code = 0x00000000 [i] Send command to Trusted App CMD_DECRYPT_BLOCK [+] OS return code = 0x00000000, TA return code = 0x00000000 [i] Send command to Trusted App CMD_DECRYPT_BLOCK [+] OS return code = 0x00000000, TA return code = 0x00000000 [i] Send command to Trusted App CMD_DECRYPT_BLOCK [+] OS return code = 0x00000000, TA return code = 0x00000000 [i] Send command to Trusted App CMD_DECRYPT_BLOCK [+] OS return code = 0x00000000, TA return code = 0x00000000 [i] Send command to Trusted App CMD_DECRYPT_BLOCK [+] OS return code = 0x00000000, TA return code = 0x00000000 [i] Send command to Trusted App CMD_DECRYPT_BLOCK [+] OS return code = 0x00000000, TA return code = 0x00000000 [i] Send command to Trusted App CMD_DECRYPT_BLOCK [+] OS return code = 0x00000000, TA return code = 0x00000000 [i] Send command to Trusted App CMD_DECRYPT_BLOCK [+] OS return code = 0x00000000, TA return code = 0x00000000 [i] Send command to Trusted App CMD_DECRYPT_BLOCK [+] OS return code = 0x00000000, TA return code = 0x00000000 [i] Send command to Trusted App CMD_DECRYPT_BLOCK [+] OS return code = 0x00000000, TA return code = 0x00000000 [i] Send command to Trusted App CMD_DECRYPT_BLOCK [+] OS return code = 0x00000000, TA return code = 0x00000000 [i] Unload TA form TrustedOS [+] OS return code = 0x00000000, TA return code = 0x00000000
We can try to summarize the program behavior using the previous output :
- loads the second binary
TA.elf.signed(for Trusted App) into the TrustedOS ; - retieves the version of the TA by sending
CMD_GET_TA_VERSIONcommand ; - checks the password, note that the check is realized in TEE ;
- asks the TA to decrypt a block with the
CMD_DECRYPT_BLOCKcommand, repeats until whole file is decrypted ; - asks the TEE to unload the TA.
Let’s take a peek and the decrypted file and see what we can learn from it :
/challenges/riscy_zones $ xxd test 0000000: 4465 6372 7970 7465 6420 626c 6f63 6b0a Decrypted block. 0000010: 4465 6372 7970 7465 6420 626c 6f63 6b0a Decrypted block. 0000020: 4465 6372 7970 7465 6420 626c 6f63 6b0a Decrypted block. 0000030: 4465 6372 7970 7465 6420 626c 6f63 6b0a Decrypted block. 0000040: 4465 6372 7970 7465 6420 626c 6f63 6b0a Decrypted block. 0000050: 4465 6372 7970 7465 6420 626c 6f63 6b0a Decrypted block. 0000060: 4465 6372 7970 7465 6420 626c 6f63 6b0a Decrypted block. 0000070: 4465 6372 7970 7465 6420 626c 6f63 6b0a Decrypted block. 0000080: 4465 6372 7970 7465 6420 626c 6f63 6b0a Decrypted block. 0000090: 4465 6372 7970 7465 6420 626c 6f63 6b0a Decrypted block. 00000a0: 4465 6372 7970 7465 6420 626c 6f63 6b0a Decrypted block. 00000b0: 4465 6372 7970 7465 6420 626c 6f63 6b0a Decrypted block. 00000c0: 4465 6372 7970 7465 6420 626c 6f63 6b0a Decrypted block. 00000d0: 4465 6372 7970 7465 6420 626c 6f63 6b0a Decrypted block. 00000e0: 4465 6372 7970 7465 6420 626c 6f63 6b0a Decrypted block. 00000f0: 4465 6372 7970 7465 6420 626c 6f63 6b0a Decrypted block. 0000100: 1010 1010 1010 1010 1010 1010 1010 1010 ................
This output suggests that the size of a block is 16 bytes. Also, we notice that the decrypted file is smaller than the encrypted one which may imply that some kind of header/footer is present.
At this point, the goal of the challenge is pretty straight forward. We’ll have to reverse engineer both binaries to understand how they communicate with each others and in then find a weakness in the encryption mechanism.
Communication with the TrustedOS :
Communication with the TEE is realized through ioctl messages with the following structure (from /challenge/tools/tee_client.py on the vm) :
class tee_message(ctypes.Structure):
CMD_GET_VERSION = 0x0001
CMD_LOAD_TA = 0x0002
CMD_TA_MESSAGE = 0x0003
CMD_UNLOAD_TA = 0x0004
CMD_CHECK_LUM = 0x0005
CMD_CHECK_KEY = 0x0006
MAX_LEN = 8192
_fields_ = [
('cmd', ctypes.c_int),
('data_in_len', ctypes.c_int),
('data_in', ctypes.c_char_p),
('data_out_len', ctypes.c_int),
('data_out', ctypes.c_char_p),
]
We recognize a few commands displayed previously in the trustzone_decrypt output. What currently remains unknown is the TA_MESSAGE structure in order to communicate with the TrustedApp. We will see shorlty that this structure is in fact very straight forward and that we could’ve found it with a little bit of black box interaction with the TrustedApp.
TA.elf.signed :
As mentionned earlier, TA.elf.signed is executed in the TEE, which means he should be compiled for the RiscV architecture :
~ $ file /challenges/riscy_zones/TA.elf.signed /challenges/riscy_zones/TA.elf.signed: ELF 32-bit LSB executable, UCB RISC-V, version 1 (SYSV), statically linked, not stripped
Encountering exotic architectures has become a common thing over the years while trying to solve the SSTIC challenges (ST20, EFI, ia64, Openrisk1000, RiscV last 3 years).
Most of the time, the necessary tools aren’t available to help you in the process of reverse engineering these binaries. Fortunately, there is always someone faster than me who comes accross these difficulities and develops the according processor for IDA before I even start looking at it.
This year, my thanks goes to Guillaume Jeanne as I found the appropriate IDA disassemblers for both Openrisk1000 and RISC-V CPUs on his github repository.
After a quick look at the RISC-V specifications, we can dive into the binary and learn that the TrustedApp implements 5 commands accessible via a jump table stored in the .rodata section :
Taking a closer look allows us to behavior of each of these commands :
The CMD_TA_INIT command is executed when the TrustedApp is loaded into the TrustedOS. This command inserts 2 hardcoded keys into the TrustedOS‘s keystore :
- SSTIC_AES_KEY whose value is “___SSTIC_2017___” ;
- SSTIC_PASSWORD_HMAC_KEY whose value is 7F DC B9 86 05 87 67 EC 47 F4 17 EF BE 85 A1 0C.
.text:00011B98 CMD_TA_INIT: .text:00011B98 lui a0, 10h .text:00011B9C addi a0, a0, 90h ; "[DEBUG] CMD CMD_TA_INIT\r\n" .text:00011BA0 jal ra, PrintAndExit .text:00011BA4 lui a1, 10h .text:00011BA8 lui a0, 10h .text:00011BAC addi a1, a1, 0ACh .text:00011BB0 addi a3, zero, 0 .text:00011BB4 addi a2, zero, 10h .text:00011BB8 addi a0, a0, 0C0h .text:00011BBC jal ra, TEE_writekey .text:00011BC0 lui a1, 10h .text:00011BC4 lui a0, 10h .text:00011BC8 addi a3, zero, 1 .text:00011BCC addi a2, zero, 10h .text:00011BD0 addi a1, a1, 0D0h .text:00011BD4 addi a0, a0, 0E4h .text:00011BD8 jal ra, TEE_writekey .text:00011BDC jal zero, Leave
I didn’t bother taking a look at the CMD_GET_TA_VERSION command. The name of the function is seft explanatory and the previous execution trace of the userland binary trustzone_decrypt suggests that the command simply retrieves the TrustedApp‘s version number. Note that I could’ve missed something here but it wasn’t mandatory in order to solve the challenge in the end.
The command CMD_CHECK_PASSWORD is much more interesting. This function starts by asking the TrustedOS to decrypt its input with the TEE_AES_decrypt syscall and the SSTIC_AES_KEY previously mentionned :
.text:00011A40 addi a2, s0, 18h ; hmac_start .text:00011A44 addi a1, sp, 40h ; a1 <= sp+0x40 => buffer_dest .text:00011A48 addi a3, s1, 0 ; a3 <= 0x70 .text:00011A4C addi a0, a0, 0C0h ; a0 <= 100C0 "SSTIC_AES_KEY" .text:00011A50 jal ra, TEE_AES_decrypt
Then, it checks that the decrypted data has the following form thanks to hardcoded strings into the .rodata section :
==BEGIN PASSWORD HMAC==
HMAC
==END PASSWORD HMAC==
Where HMAC is a 256 bits hash.
.text:00011A54 lui a1, 10h .text:00011A58 addi a2, zero, 19h ; a2 <= 0x19 .text:00011A5C addi a1, a1, 164h ; a1 <= 0x10164 ==BEGIN PASSWORD HMAC== .text:00011A60 addi a0, sp, 40h ; a0 <= sp+0x40 (hmac_decrypted_start) .text:00011A64 addi s0, s0, 6 ; s0 <= password_decoded_start .text:00011A68 jal ra, checkIfEqual .text:00011A6C bne loc_11CBC, a0, zero ; goto fail : "bad hmac blob" .text:00011A70 addi a0, s1, -17h .text:00011A74 lui a1, 10h .text:00011A78 addi a5, sp, 40h .text:00011A7C addi a2, zero, 17h .text:00011A80 addi a1, a1, 198h ; 10198 \r\n==END PASSWORD HMAC== .text:00011A84 add a0, a5, a0 .text:00011A88 jal ra, checkIfEqual .text:00011A8C bne loc_11CBC, a0, zero ; goto fail
Finally, the commands asks the TrustedOS to compute the password’s HMAC with the SSTIC_PASSWORD_HMAC_KEY key and compares it to the HMAC extracted from the decrypted data. If the password is correct, it is inserted into the TrustedOS’s keystore.
The CMD_DECRYPT_BLOCK is a little more complicated. The function expects a 128 bits data input to encrypt along with the number of the block which will be used in the key diffusion algorithm.
My understanding of the algorithm (as I recall, because it’s been a while since I did that challenge now) is as such :
- Key diffusion – Part 1
The key is split in four 32 bits parts and the following diffusion algorithm is applied to each the parts :
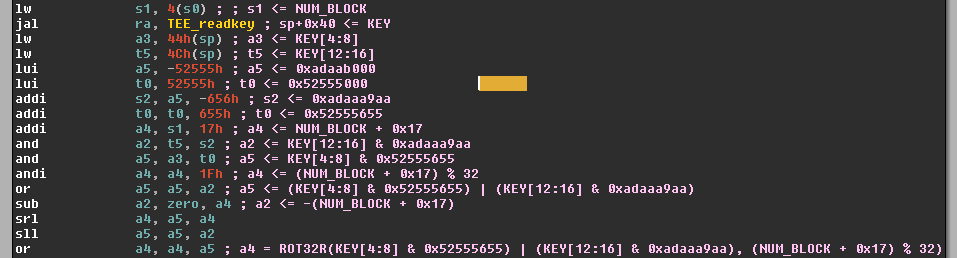
Pretty much the same method is applied to the others parts of the initial key, at the end the this process we obtain the following four 32 bits derivated keys :
MASK_1 = 0x52555655 MASK_2 = 0xadaaa9aa dKEY0 = ROT32R(KEY04 & MASK_1 | KEY12 & MASK_2, (0x17 + NUM_BLOCK) % 32); dKEY1 = ROT32R(KEY00 & MASK_1 | KEY08 & MASK_2, (0x13 + NUM_BLOCK) % 32); dKEY2 = ROT32R(KEY04 & MASK_2 | KEY12 & MASK_1, (0x11 + NUM_BLOCK) % 32); dKEY3 = ROT32R(KEY00 & MASK_2 | KEY08 & MASK_1, (0xd + NUM_BLOCK) % 32);
- Key diffusion – Part 2
- Encryption
- Pi is the decrypted block of index i ;
- Ci is the ciphered block of index i ;
- d(KEY, round) is the derivation key algorithm seen in 1 and 2.
The second part of the diffusion is as such :
inc = 0 # accumulator 1 w = 0x41 # # accumulator 2 inc = (tKEY0>>0x18) + w inc &= 0xff NEXTKEY = chr(inc) + NEXTKEY w += 0x7 inc += ((tKEY0>>0x10) & 0xff) + w inc &= 0xff NEXTKEY = chr(inc) + NEXTKEY w += 0x7 inc += ((tKEY0>>0x8) & 0xff) + w inc &= 0xff NEXTKEY = chr(inc) + NEXTKEY w += 0x7 inc += (tKEY0 & 0xff) + w inc &= 0xff NEXTKEY = chr(inc) + NEXTKEY w += 0x7
The following assembly shows the assembly code responsible for the processing of the first bytes of dKEY0 :
As you may notice, a few instructions are sometimes inserted in the middle of a couple of instructions responsible for the processing of a certain operation, which makes it harder to get a big picture of what’s actually going on.
This process is repeated with the dKEY1, dKEY2, dKEY3 (in that order). In the end, we have a new 128 bits key derivated from the former one and the number of the current round.
The encryption/decryption mechanism is close to the CBC mode, we have :
Pi = d(KEY , round) ^ Ci ^ reverse(Ci -1)
Where :
The solution :
The encryption algorithm gives us, for the first block :
P0 = d(KEY , 0) ^ C0 ^ reverse(IV)
At this point, we already know the values of :
- C0 ;
- reverse(IV).
When we take a closer look at the encrypted file, we notice that its name implies that we’re expecting an lzma archive after decrypting it. This information proves useful because like every file format, an lzma archive has a recognizable header. In particular, if we take the assumption that the default parameters were used during the compression, of the 16 bytes of the first clear text block, only 2 are left unknown. Indeed, with the default compression, the first 14 bytes of a lzma archive are those : 5D 00 00 80 00 FF FF FF FF FF FF FF FF 00. This approach is called a known-plaintext attack.
There are several ways of solving the challenge at this point. My solution was to revert the key derivation algorithm in order to develop the following function :
def r(C, P, IV):
# returns a 128 bits key
Where :
- C is an encrypted block ;
- P is a plain-text block ;
- IV is an initialization vector.
The function returns the KEY that was used in order to have :
P = d(KEY , 0) ^ C ^ reverse(IV)
Once we have this function, all we have to do is to generate all the possible keys by bruteforcing the 2 unknowns bytes of the plain-text.
Put it simply, inverting an algorithm is executing the instructions in the reverse order, which means we have to start with the second phase of the key diffusion, then the first one.
- Inversion of the 2nd part of the key diffusion
- Inversion of the 1st part of the key diffusion
- Getting the actual key
The 2nd part of the diffusion is pretty straight forward, we start by the end of the block and simply execute the opposite of what’s done in the key diffusion (repeat a XOR to cancel the first one, sub<->add, ROT32L<->ROT32R). With simples instructions like that we can retrieve the temporary keys obtained at the end of the first part of the key diffusion. The python sample below processes these operations for the first temporary key :
# KEY 0 x = ord(PLAIN[15]) ^ ord(CIPHER[15]) ^ ord(IV[0]) tKEY0_18 = (x - SUM) & 0xff SUM += dKEY0_18 + 0x48 x = ord(PLAIN[14]) ^ ord(CIPHER[14]) ^ ord(IV[1]) tKEY0_10 = (x - SUM) & 0xff SUM += dKEY0_10 + 0x4F x = ord(PLAIN[13]) ^ ord(CIPHER[13]) ^ ord(IV[2]) tKEY0_8 = (x - SUM) & 0xff SUM += dKEY0_8 + 0x56 x = ord(PLAIN[12]) ^ ord(CIPHER[12]) ^ ord(IV[3]) tKEY0_0 = (x - SUM) & 0xff SUM += dKEY0_0 + 0x5d dKEY0 = (dKEY0_18 << 0x18) + (dKEY0_10 << 0x10) + (dKEY0_8 << 0x8) + dKEY0_0
We end up with the same temporary keys as we did at the end of the fist phase of the key diffusion, here’s a quick reminder :
MASK_1 = 0x52555655 MASK_2 = 0xadaaa9aa dKEY0 = ROT32R(KEY04 & MASK_1 | KEY12 & MASK_2, (0x17 + NUM_BLOCK) % 32); dKEY1 = ROT32R(KEY00 & MASK_1 | KEY08 & MASK_2, (0x13 + NUM_BLOCK) % 32); dKEY2 = ROT32R(KEY04 & MASK_2 | KEY12 & MASK_1, (0x11 + NUM_BLOCK) % 32); dKEY3 = ROT32R(KEY00 & MASK_2 | KEY08 & MASK_1, (0xd + NUM_BLOCK) % 32);
The opposite operation of a ROT32R is a ROT32L with the same offset, so we can trivialy retrieve these 4 values :
dKEY0 = KEY04 & 0x52555655 | KEY12 & 0xadaaa9aa dKEY1 = KEY00 & 0x52555655 | KEY08 & 0xadaaa9aa dKEY2 = KEY04 & 0xadaaa9aa | KEY12 & 0x52555655 dKEY3 = KEY00 & 0xadaaa9aa | KEY08 & 0x52555655
Now it may seem ridiculous to some, but I had a hard time solving this (ie retrieving KEY00, KEY04, KEY08, KEY12 from these equations). Let’s take a look at these masks, in binary :
>>> bin(0x52555655) '0b1010010010101010101011001010101' >>> bin(0xadaaa9aa) '0b10101101101010101010100110101010'
Notice anything? Let’s put these values next to each others :
01010010010101010101011001010101 (0x52555655) 10101101101010101010100110101010 (0xadaaa9aa)
Yup, these values are complimentary to each others. Indeed, we have :
>>> 0x52555655 & 0xadaaa9aa 0
Let’s try this :
dKEY1 & 0x52555655
<=> (KEY00 & 0x52555655 | KEY08 & 0xadaaa9aa) & 0x52555655
<=> [(KEY00 & 0x52555655) & 0x52555655] | [(KEY08 & 0xadaaa9aa) & 0x52555655]
<=> (KEY00 & 0x52555655) | (KEY08 & 0)
<=> KEY00 & 0x52555655
And :
dKEY3 & 0xadaaa9aa
<=> (KEY00 & 0xadaaa9aa | KEY08 & 0x52555655) & 0xadaaa9aa
…
<=> (KEY00 & 0xadaaa9aa)
We get :
(KEY00 & 0x52555655) | (KEY00 & 0xadaaa9aa)
<=> KEY00
There, we have what we want, we’re able to retrieve KEY00 from the four equations. By repeating these operations we obtain the rest of the parts of the initial key :
KEY00 = (dKEY1 & 0x52555655)|(dKEY3 & 0xadaaa9aa) KEY04 = (dKEY0 & 0x52555655)|(dKEY2 & 0xadaaa9aa) KEY08 = (dKEY1 & 0xadaaa9aa)|(dKEY3 & 0x52555655) KEY12 = (dKEY0 & 0xadaaa9aa)|(dKEY2 & 0x52555655)
Here’s the full code of the function :
def inverse(CIPHER, PLAIN, IV):
SUM = 0x41
# KEY 0
x = ord(PLAIN[15]) ^ ord(CIPHER[15]) ^ ord(IV[0])
dKEY0_18 = (x - SUM) & 0xff
SUM += dKEY0_18 + 0x48
x = ord(PLAIN[14]) ^ ord(CIPHER[14]) ^ ord(IV[1])
dKEY0_10 = (x - SUM) & 0xff
SUM += dKEY0_10 + 0x4F
x = ord(PLAIN[13]) ^ ord(CIPHER[13]) ^ ord(IV[2])
dKEY0_8 = (x - SUM) & 0xff
SUM += dKEY0_8 + 0x56
x = ord(PLAIN[12]) ^ ord(CIPHER[12]) ^ ord(IV[3])
dKEY0_0 = (x - SUM) & 0xff
SUM += dKEY0_0 + 0x5d
dKEY0 = (dKEY0_18 << 0x18) + (dKEY0_10 << 0x10) + (dKEY0_8 << 0x8) + dKEY0_0
dKEY0 = ROT32L(dKEY0, 0x17)
# KEY 1
x = ord(PLAIN[11]) ^ ord(CIPHER[11]) ^ ord(IV[4])
dKEY1_18 = (x - SUM) & 0xff
SUM += dKEY1_18 + 0x64
x = ord(PLAIN[10]) ^ ord(CIPHER[10]) ^ ord(IV[5])
dKEY1_10 = (x - SUM) & 0xff
SUM += dKEY1_10 + 0x6b
x = ord(PLAIN[9]) ^ ord(CIPHER[9]) ^ ord(IV[6])
dKEY1_8 = (x - SUM) & 0xff
SUM += dKEY1_8 + 0x72
x = ord(PLAIN[8]) ^ ord(CIPHER[8]) ^ ord(IV[7])
dKEY1_0 = (x - SUM) & 0xff
SUM += dKEY1_0 + 0x79
dKEY1 = (dKEY1_18 << 0x18) + (dKEY1_10 << 0x10) + (dKEY1_8 << 0x8) + dKEY1_0
dKEY1 = ROT32L(dKEY1, 0x13)
# KEY 2
x = ord(PLAIN[7]) ^ ord(CIPHER[7]) ^ ord(IV[8])
dKEY2_18 = (x - SUM) & 0xff
SUM += dKEY2_18 + 0x80
x = ord(PLAIN[6]) ^ ord(CIPHER[6]) ^ ord(IV[9])
dKEY2_10 = (x - SUM) & 0xff
SUM += dKEY2_10 + 0x87
x = ord(PLAIN[5]) ^ ord(CIPHER[5]) ^ ord(IV[10])
dKEY2_8 = (x - SUM) & 0xff
SUM += dKEY2_8 + 0x8e
x = ord(PLAIN[4]) ^ ord(CIPHER[4]) ^ ord(IV[11])
dKEY2_0 = (x - SUM) & 0xff
SUM += dKEY2_0 + 0x95
dKEY2 = (dKEY2_18 << 0x18) + (dKEY2_10 << 0x10) + (dKEY2_8 << 0x8) + dKEY2_0
dKEY2 = ROT32L(dKEY2, 0x11)
# KEY 3
x = ord(PLAIN[3]) ^ ord(CIPHER[3]) ^ ord(IV[12])
dKEY3_18 = (x - SUM) & 0xff
SUM += dKEY3_18 + 0x9c
x = ord(PLAIN[2]) ^ ord(CIPHER[2]) ^ ord(IV[13])
dKEY3_10 = (x - SUM) & 0xff
SUM += dKEY3_10 + 0xa3
x = ord(PLAIN[1]) ^ ord(CIPHER[1]) ^ ord(IV[14])
dKEY3_8 = (x - SUM) & 0xff
SUM += dKEY3_8 + 0xaa
x = ord(PLAIN[0]) ^ ord(CIPHER[0]) ^ ord(IV[15])
dKEY3_0 = (x - SUM) & 0xff
dKEY3 = (dKEY3_18 << 0x18) + (dKEY3_10 << 0x10) + (dKEY3_8 << 0x8) + dKEY3_0
dKEY3 = ROT32L(dKEY3, 0xd)
KEY0 = (dKEY1 & 0x52555655)|(dKEY3 & 0xadaaa9aa)
KEY1 = (dKEY0 & 0x52555655)|(dKEY2 & 0xadaaa9aa)
KEY2 = (dKEY1 & 0xadaaa9aa)|(dKEY3 & 0x52555655)
KEY3 = (dKEY0 & 0xadaaa9aa)|(dKEY2 & 0x52555655)
return struct.pack('<I',KEY0) + struct.pack('<I',KEY1) + struct.pack('<I',KEY2) + struct.pack('<I',KEY3)
As said earlier, once we’re able to invert the key diffusion algorithm, all that’s left to do is generating every key by bruteforcing the plaintext block (2 bytes -> 65536 possibilities) and pray that the default parameters were used during the compression of the lzma archive.
Once we have these keys, you can feed them one after the other with a small script until the right one is found and let the program decrypt the file :
/challenges/riscy_zones $ ./trustzone_decrypt 5921cd9fd3a82bd9244ece5328c6c95f secret.lzma.encrypted secret.lzma [i] load TA.elf.signed in TrustedOS [+] OS return code = 0x00000000, TA return code = 0x00000000 [i] Send command to Trusted App CMD_GET_TA_VERSION [+] OS return code = 0x00000000, TA return code = 0x00000000 retreived version : SSTIC Trusted APP v0.0.1 [i] check password in TEE [+] OS return code = 0x00000000, TA return code = 0x00000000 Good password ! [i] Send command to Trusted App CMD_DECRYPT_BLOCK [+] OS return code = 0x00000000, TA return code = 0x00000000 [i] Send command to Trusted App CMD_DECRYPT_BLOCK [+] OS return code = 0x00000000, TA return code = 0x00000000 [i] Send command to Trusted App CMD_DECRYPT_BLOCK [+] OS return code = 0x00000000, TA return code = 0x00000000 [i] Send command to Trusted App CMD_DECRYPT_BLOCK [+] OS return code = 0x00000000, TA return code = 0x00000000 [i] Send command to Trusted App CMD_DECRYPT_BLOCK [+] OS return code = 0x00000000, TA return code = 0x00000000 [i] Send command to Trusted App CMD_DECRYPT_BLOCK [+] OS return code = 0x00000000, TA return code = 0x00000000 [i] Send command to Trusted App CMD_DECRYPT_BLOCK [+] OS return code = 0x00000000, TA return code = 0x00000000 [...]
The decrypted archive contains the following image :
Final notes :
This was the 3rd level of the challenge (out of 5) and overall my favorite. I really encourage you into giving it a try. Hope you enjoyed it as much as I did. Thanks again to everyone involved in the creation of this challenge and see you next year.



Be First to Comment